exoticjilo.blogg.se

• #Vertical compression exampes how to#

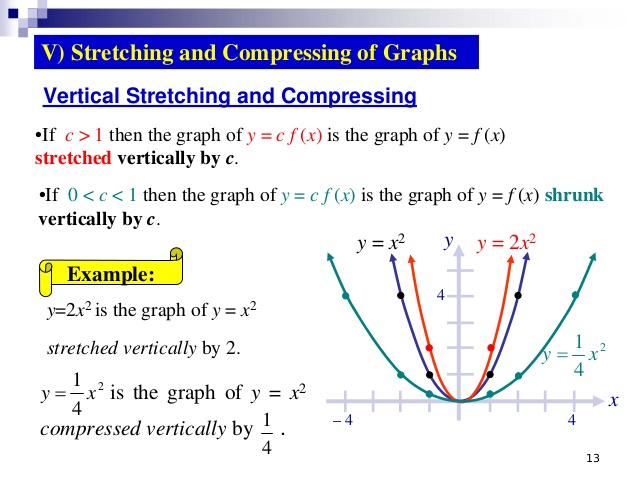
This means the larger the absolute value of m, the steeper the slope. If the constant is greater than 1, we get a vertical stretch if the constant is between 0 and 1.

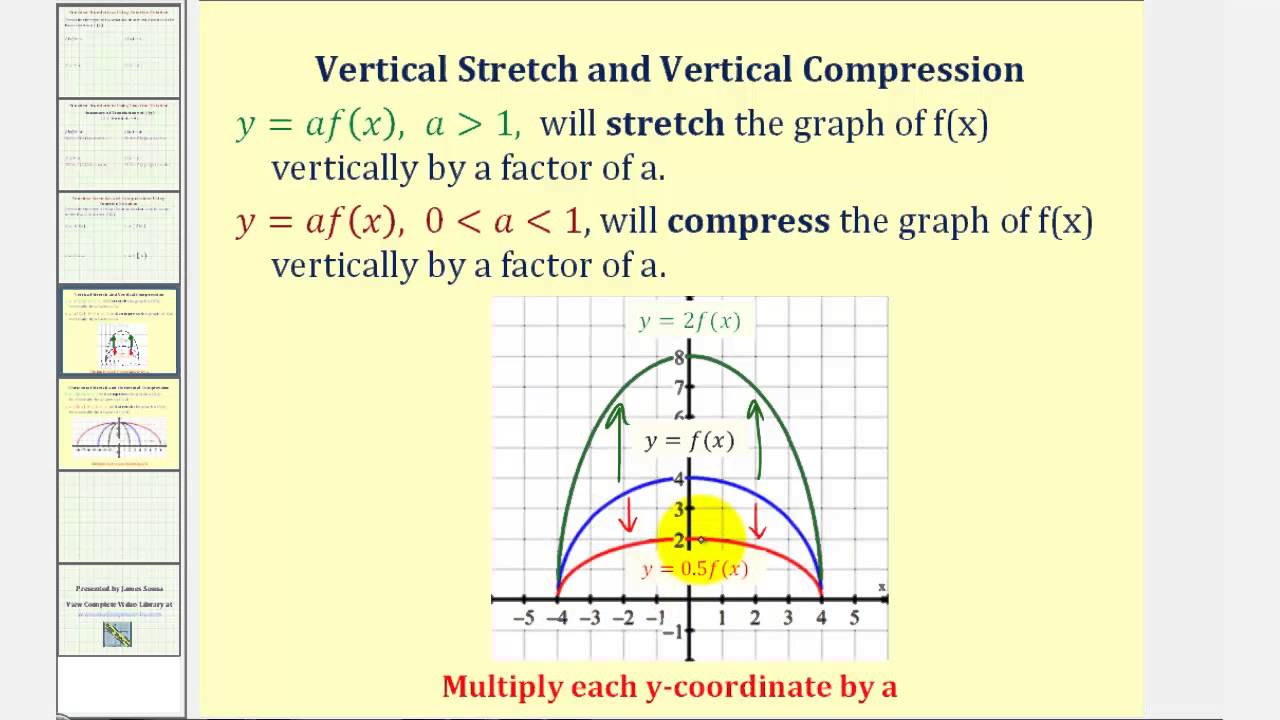
Notice in the figure below that multiplying the equation of f\left(x\right)=x by m vertically stretches the graph of f by a factor of m units if m>1 and vertically compresses the graph of f by a factor of m units if 0function may also be transformed using a reflection, stretch, or compression. A function may be transformed by a shift up, down, left, or right. What is a vertical compression Vertical compressions occur when a function is multiplied by a rational scale factor. We’ll also apply our knowledge on vertical compressions by graphing different types of functions.

#Vertical compression exampes how to#

Graphing a Linear Function Using TransformationsĪnother option for graphing linear functions is to use transformations of the identity function f\left(x\right)=x. This article will show how to identify vertical compressions given two or more functions’ expressions and graphs. Use simple transformations to graph linear functions.